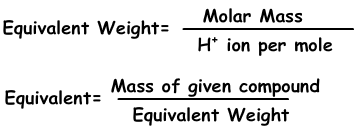Concentration with Examples
Concentration
Concentration is the amount of solute in given solution. We can express concentration in different ways like concentration by percent or by moles.
1) Concentration by Percent:
It is the amount of solute dissolves in 100 g solvent. If concentration of solution is 20 %, we understand that there are 20 g solute in 100 g solution.
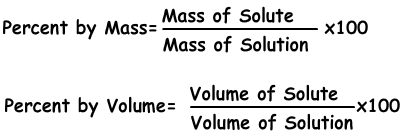
Example: 10 g salt and 70 g water are mixed and solution is prepared. Find concentration of solution by percent mass.
Solution:
Mass of Solute: 10 g
Mass of Solution: 10 + 70 = 80 g
80 g solution includes 10 g solute
100 g solution includes X g solute
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
X=12,5 g %
Or using formula;
Percent by mass=10.100/80=12,5 %
Example: If concentration by mass of 600 g NaCl solution is 40 %, find amount of solute by mass in this solution.
Solution:
100 g solution includes 40 g solute
600 g solution includes X g solute
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
X=240 g NaCl salt dissolves in solution.
Example: If we add 68 g sugar and 272 g water to 160 g solution having concentration 20 %, find final concentration of this solution.
Solution:
Mass of solution is 160 g before addition sugar and water.
100 g solution includes 20 g sugar
160 g solution includes X g sugar
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
X=32 g sugar
Mass of solute after addition=32 + 68=100 g sugar
Mass of solution after addition=272 +68 + 160=500 g
500 g solution includes 100 g sugar
100 g solution includes X g sugar
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
X= 20 % is concentration of final solution.
2) Concentration by Mole:
We can express concentration of solutions by moles. Number of moles per liter is called molarity shown with M.
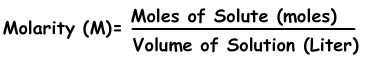
Example: Using 16 g NaOH, 200 ml solution is prepared. Which ones of the following statements are true for this solution?(Molar mass of NaOH is 40 g)
I. Concentration of solution is 2 molar
II. Volume of the water in solution is 200 ml
III. If we add water to solution, moles of solute decreases.
Solution: Moles of NaOH
I. nNaOH=16/40=0,4 mole
V=200 mL= 0,2 Liters
Molarity=0,4/0,2=2 molar
I is true
II. Since volume of solution is 200 mL, volume of water is smaller than 200 mL. II is false.
III. If we add water to solution, volume of solution increases but moles of solute does not change.
Example: 4,4 g XCl2 salt dissolves in water and form 100 ml 0,4 molar XCl2 solution. Find molar mass of X. (Cl=35)
Solution:
Molarity=n/V
n=M.V where V=100mL=0,1 L and M=0,4 molar
n=0,1.0,4=0,04 mole
If 0,04 mole XCl2 is 4,4 g
1 mole XCl2 is ? g
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
?=110 g XCl2
Molar mass of XCl2=X+2.(35)=110
X=40 g/mole
3) Molality:
Molality is the another expression of concentration of solutions. It is denoted with “m” and formula of molality is;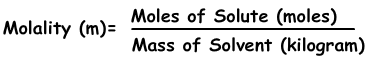
4) Normality:
We can express concentration in another way with normality using equivalents of solutes.

Equivalents can be defined as; number of moles of H+ ion in acids and OH- ion in base reactions. For example; 1 mole H2SO4 gives 2 H+ ion, equivalent of H2SO4 is 2. We find equivalent weight;