Chemical Equilibrium
Chemical Equilibrium
Until now, we have learned that reactions take place in one direction. But now we deal with reversible reactions. Reaction, given below, is in closed container;
A(g) + B(g) → C(g) + D(g)
At the beginning, A reacts with B and produce C and D gas. This is forward reaction and rate of this reaction is written as;
Reaction Rate= kf.[A].[B]
Since concentrations of A and B decrease with time, forward reaction rate also decreases. Moreover, produced C and D molecules collide to each other and form A and B molecules. This is called reverse reaction and rate of it is written as;
Reaction Rate= kr.[C].[D]
Concentrations of C and D gases increases and A and B decreases with time. At one point reaction rates of forward and reverse reaction becomes equal and reaction reaches equilibrium. We write this equations like;
kf.[A].[B] = kr.[C].[D]
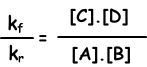
kf/kr=equilibrium constant and represented with Kc in terms of concentration. Equilibrium constant of following reaction is written as;
aA + bB ↔ cC + dD
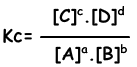
Equilibrium equation is written from total reaction. We do not concern steps of reactions as in the case of one direction reactions. Reactions must obey following rules to reach equilibrium;
- System must be closed
- Temperature must be constant
- Reaction must be reversible
If temperature changes, then reaction rates of forward or reverse can be changed and system do not reach equilibrium. If reaction is not reversible we can not talk about equilibrium. Finally, closed systems required to prevent matter loss during reaction. Now we learn why systems tend to reach equilibrium.
- All systems want to decrease their energy. It is the tendency of minimal energy.
- All systems tend to increase their disorder. It is called as tendency of maximum disorder.
Water in a open container evaporates with time. Liquid water has lower energy than gas water and obey minimal energy law. On the contrary, vaporization of it can be explained by maximum disorder law. Liquid water molecules change their phase to gas and increase their disorder.
Disorder of;
Gas > Solutions > Liquid > Solid
Energy of ;
Gas > Liquid >Solid
P.S:
Dissolution of solids and liquids are exothermic or endothermic. However, dissolution of gases are always exothermic.
Example: Which ones of the following reactions can be exothermic?
I. 2HI(g) ↔ H2(g) + I2(g)
II. 2NH3(g) ↔ N2(g) + 3H2(g)
III. CO2(g) ↔ CO2(aq)
IV. CaCO3(s) ↔ CaO(s) + CO2(g)
V. N2O4(g) ↔ 2NO2(g)
Solution: I, II, and V reactions are all in gas phase. Disorder increases in products direction. So, these reactions are endothermic. In reaction IV, solid matter change phase and becomes gas. Since disorder increases from solid to gas phase, this reaction is endothermic. In reaction III, disorder increases from products to reactants and reaction is exothermic.
Homogeneous and Heterogeneous Equilibrium
If matters in equilibrium reaction are all in one phase then it is homogeneous equilibrium, if at least one of the matter has different phase then it is heterogeneous equilibrium.
When we write equilibrium equation of heterogeneous equilibrium,we do not write pure solid and pure liquid matters in equilibrium equation. For example;
2NH3(g) ↔ N2(g) + 3H2(g)
reaction is homogeneous reaction and we write all matters to equilibrium equation.
CaCO3(s) ↔ CaO(s) + CO2(g)
This reaction is heterogeneous equilibrium reaction and we do not write CaCO3(s) and CaO(s) in equilibrium equation.
Equilibrium Constant in terms of Partial Pressure
Concentrations of gases are directly proportional to partial pressure of them. Thus, we can write equilibrium constant in terms of partial pressures.
N2(g) + 3H2(g) ↔ 2NH3(g)
Equilibrium constant of this reaction in terms of concentrations is;
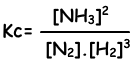
Equilibrium constant of this reaction in terms of partial pressure is;
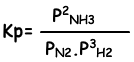
Relation between these two equilibrium constant is;
Kp=Kc(R.T)∆n
∆n= ∑nreactants - ∑nproducts
For example:
N2(g) + 3H2(g) ↔ 2NH3(g)
Since ∆nproducts=2 (2 mol NH3) and ∆nreactants=4 (1 mol N2 and 3 mol H2)
∆n= -2
Kp=Kc.(R.T)-2