Dilution and Density of Solutions

Dilution and Density of Solutions

Dilution is process of adding solvent to solution. Since amount of solute stays constant, concentration of solution decreases. We find relation between concentration of solutions before and after dilution with following formula;

M₁.V₁=M₂.V₂

Where M₁ is initial molarity and M₂ is final molarity and V₁ and V₂ are initial and final volumes of solution.

To increase concentration of solutions, you should add solute or evaporate solvent from solution. Formula given above is also used in increasing concentration of solutions;

M₁.V₁=M₂.V₂

Concentration of solutions and volumes are inversely proportional to each other. If volume of solution increases then, molarity of solution decreases. Graph given below shows this relation;

Example: If we add 700 mL water at same temperature to 0,2 molar 300 mL solution, find final molar concentration of this solution.

Solution:

M₁=0,2 molar, V₁=300=0,3 mL

V₂=300+700 =1000mL=1 L

M₁.V₁=M₂.V₂

0,2.0,3=M₂.1

M₂=0,06 molar

Example: If we mix solutions given in the picture below, find concentration of final solution.

Solution: Sum of masses solution one and two gives us mass of final solution

m₁+m₂=m_final

80 + 40 =120 g

Sum of solute masses  one and two gives us mass of final solute.

(1) m_sugar1 + m_sugar2=m_sugarf

We find masses of solutes by;

m_sugar1=m₁.20/100=80.1/5=16 g

m_sugar2=m₂.30/100=40.30/100=12 g

m_sugarf=m_final.X/100=120.X/100 g

we use equation (1) and solve for X;

m_sugar1 + m_sugar2=m_sugarf

16 + 12=120.X/100 g

28=12.X/10

X=23,3

Density of Solutions

We find density of solutions by following formula;

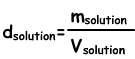
Unit of liquid solutions g/mL or g/cm³. Putting solute into water we prepare solution. When we add solute to solution density of it increases, since increase in the mass of solution is larger than the increase in volume. In solid-liquid solutions, density increases with increasing in the concentration of solution.

Example: Density of H₂SO₄ solution, having percent by mass 49 %, is 1,2 g/mL. Find molar concentration of this solution. (H₂SO₄=98)

Solution:

density of solution=1,2 g/mL

Percent by mass= 49 %

Molar mass of H₂SO₄ is 98 g

We find molar concentration of solution with following formula;

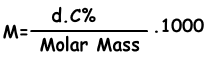
M=(1,2.4)/98 . 1000

M=6 molar

Example: Solubility of X at 15 ^oC is 20g X/100. Which ones of the following statements are true for solution prepared using 30 g X and 120 g water at 15 ^oC?

I. Solution is saturated.

II. Mass of solution is 150 g.

III. Concentration percent by mass is 20 %

Solution:

I. at 15^oC

100 g water dissolves 20 g X

120 g water dissolves ? g X

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

?=24 g X is dissolved.

since 30 g X is added to 120 g water, solution is saturated and 30-24=6 g X stays undissolved. I is true.

II. Mass of solution is equal to sum of solute and solvent.

m=msolute+msolvent

m=120+24=144

Thus mass is not equal to 150 g, II is false.

III. Since 100 g water dissolves 20 g X, there are also 20 g X in 120 g solution. Thus, percent by mass;

X %=(m_X/msolution).100

X %=(20/120).100=16,7

III is false

Solutions Exams and Problem Solutions