Density of Gases with Examples
Density of Gases with Examples
Density of gases is too small with respect to solid and gas phases. We can find density with following formula;
d(gas)=m(gas)/V(gas)
if we substitute it into the ideal gas law;
P.V=n.R.T where n=mass/molar mass
P.V=(m/Mm).R.T
P.Mm=(m/V).R.T
P.Mm=d.R.T
d=(P.Mm)/(R.T)
As you can see from the formula; density of gases is directly proportional to pressure and molar mass and inversely proportional to temperature.
Example: Find density of C4H8 at 273 0C and under 2 atm pressure. (H=1, C=12)
Solution: we make unit conventions first;
T=273+273=546 K
P=2 atm
C4H8=4.12+8.1=56 g/mol
Using formula given above;
P.Mm=d.R.T
2.56=d.(22,4/273).546
d=2,5 g/L
Example: If we add some CH4 to container given below under constant temperature; which ones of the following statements are true related to gases in this container? (He=4, C=12, H=1)

I. Density of mixture increases
II. Volume increases
III. Pressure increases
Solution:
Molar mass of CH4=12+4.1=16
Since piston of container is dynamic, when we add CH4, volume of mixture increases. Molar mass of CH4 is greater than He, thus density of mixture also increases.
P.Mm=d.R.T
Increasing in the volume of gas balance pressure and it stays constant.
Example: Which ones of the graphs are true for ideal gas.

Solution:
I. Using ideal gas law;
P.V=n.R.T
P=n.R.T/V
Since R, n and V are constant, P is directly proportional to temperature. Graph I is true.
II. Molar volume is V/n. Using ideal gas law;
V/n=R.T/P
Since R, P and T are constant V/n must be constant. Thus second graph is false, line showing relation between V and n must be parallel to n.
III. We write ideal gas law for density;
d=P.Mm/R.T
Mm, R and P are constant , thus d is inversely proportional to T. III. graph is true.
Example: Graph given below shows density vs. volume relation of X(gas) at 00C. If the pressure of X(gas) at point A is 1 atm, which ones of the following statement are true for this gas.

I. n=1mol
II. Pressure at point B is 0,5 atm
III. Molar mass of gas is 56 g
Solution:
I. Ideal gas law at point A;
PA.VA=n.R.T
T=0 0C or 273 K
V=11,2 Liters
P=1 atm
n=PA.VA/R.T=(1.11,2)/(22,4/273).273)=0,5mol
I is false.
II. n and T are constant, thus we can write;
PA.VA=PB.VB
(1.11,2)=PB.22,4
PB=0,5 atm, II is true
III. density at point A is;
dA=PA.Mm/R.T
Mm=(dA.R.T)/PA=(2,5.(22,4/273).273)/1
Mm=56 g/mol
1 mol gas contains 56 g, so III is true.
Example: Which ones of the following statements are true for He and O2 gases under same temperature. (He=4, O=16)
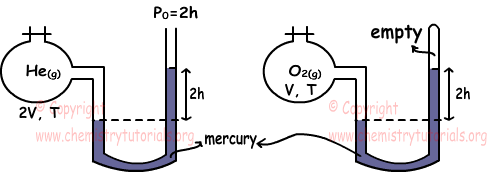
I. nHe=4nO2
II. dHe=8dO2
III. Average kinetic energies of He and O2 are equal.
Solution:
We find pressures of gases using manometers.
PHe=2h+2h=4h
PO2=2h
To find relation between number of moles of gases we use ideal gas law.
PHe.VHe=nHe.R.THe
nHe=4h.2V/R.T
PO2.VO2=nO2.R.TO2
nO2=2h.V/R.T
Ratio of nHe and nO2
nHe/nO2=4/1 Thus, I is true.
We find density of gases again using ideal gas law.
Molar mass of He=4 and Molar mass of O2=2.16=32
dHe=PHe.MHe/R.T
dHe=4h.4/R.T
dO2=PO2.MO2/R.T
dO2=2h.32/R.T
Ratio de las densidades;
dHe/d/O2=1/4 so, II is false.
III. Since temperature of gases same, their average kinetic energies are also same. III is true.