Chemisch Evenwicht
Chemisch Evenwicht
Tot nu toe hebben we geleerd dat reacties in één richting plaatsvinden. Maar nu behandelen we omkeerbare reacties. Reactie, hieronder gegeven, bevindt zich in een gesloten container;
A(g) + B(g) → C(g) + D(g)
In het begin reageert A met B en produceert C en D gas. Dit is een voorwaartse reactie en de snelheid van deze reactie wordt geschreven als;
Reactiesnelheid = kf.[A].[B]
Omdat concentraties van A en B met de tijd afnemen, neemt ook de voorwaartse reactiesnelheid af. Bovendien botsen geproduceerde C en D moleculen op elkaar en vormen A en B moleculen. Dit wordt omgekeerde reactie genoemd en de snelheid ervan wordt geschreven als;
Reactiesnelheid = kr.[C].[D]
Concentraties van C en D gassen nemen toe en A en B nemen af met de tijd. Op een gegeven moment worden reactiesnelheden van voorwaartse en achterwaartse reactie gelijk en bereikt de reactie evenwicht. We schrijven deze vergelijkingen als;
kf.[A].[B] = kr.[C].[D]
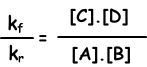
kf / kr = evenwichts constante en weergegeven met Kc in termen van concentratie. Evenwichtsconstante van de volgende reactie wordt geschreven als;
aA + bB ↔ cC + dD
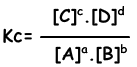
Evenwichtsvergelijking wordt geschreven uit totale reactie. We hebben geen betrekking op stappen van reacties zoals in het geval van reacties in één richting. Reacties moeten de volgende regels volgen om een evenwicht te bereiken;
- Systeem moet gesloten zijn
- Temperatuur moet constant zijn
- Reactie moet omkeerbaar zijn
Als de temperatuur verandert, kunnen de reactiesnelheden van vooruit of achteruit worden gewijzigd en bereikt het systeem geen evenwicht. Als de reactie niet omkeerbaar is, kunnen we niet over evenwicht spreken. Ten slotte waren gesloten systemen nodig om materie verlies tijdens de reactie te voorkomen. Nu leren we waarom systemen de neiging hebben om een evenwicht te bereiken.
- Alle systemen willen hun energie verminderen. Het is de neiging van minimale energie.
- Alle systemen hebben de neiging om hun stoornis te vergroten. Het wordt de neiging van maximale wanorde genoemd.
Water in een open container verdampt met de tijd. Vloeibaar water heeft minder energie dan gaswater en voldoet aan de minimale energiewet. Integendeel, verdamping ervan kan worden verklaard door maximale wanorde. Vloeibare watermoleculen veranderen hun fase in gas en vergroten hun wanorde.
Stoornis van;
Gas> Oplossingen> Vloeistof> Vast
Energie van;
Gas> Vloeistof> Vast
P.S:
Het oplossen van vaste stoffen en vloeistoffen is exotherm of endotherm. Het oplossen van gassen is echter altijd exotherm.
Voorbeeld: welke van de volgende reacties kunnen exotherm zijn?
I. 2HI(g) ↔ H2(g) + I2(g)
II. 2NH3(g) ↔ N2(g) + 3H2(g)
III. CO2(g) ↔ CO2(aq)
IV. CaCO3(s) ↔ CaO(s) + CO2(g)
V. N2O4(g) ↔ 2NO2(g)
Oplossing: I, II en V reacties bevinden zich allemaal in de gasfase. Stoornis neemt toe in de productrichting. Deze reacties zijn dus endotherm. In reactie IV verandert de vaste stoffase en wordt gas. Omdat de aandoening toeneemt van vaste naar gasfase, is deze reactie endotherm. In reactie III neemt de wanorde toe van producten tot reactanten en is de reactie exotherm.
Homogeen En Heterogene Evenwicht
Als zaken in evenwichtsreactie zich allemaal in één fase bevinden, is het homogeen evenwicht, als ten minste één van de materie een andere fase heeft, is het een heterogeen evenwicht.
Wanneer we een evenwichtsvergelijking van heterogeen evenwicht schrijven, schrijven we geen zuivere vaste en zuivere vloeibare materie in een evenwichtsvergelijking. Bijvoorbeeld;
2NH3(g) ↔ N2(g) + 3H2(g)
Reactie is een homogene reactie en we schrijven alle zaken op evenwichtsvergelijking.
CaCO3(s) ↔ CaO(s) + CO2(g)
Deze reactie is een heterogene evenwichtsreactie en we schrijven geen CaCO3 (s) en CaO (s) in evenwichtsvergelijking.
Evenwichts Constante In Termen Van Partiële Druk
Concentraties van gassen zijn recht evenredig met de partiële druk ervan. We kunnen dus evenwichtsconstante schrijven in termen van partiële drukken.
N2(g) + 3H2(g) ↔ 2NH3(g)
Evenwichts constante van deze reactie in termen van concentraties is;
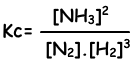
Evenwichts constante van deze reactie in termen van partiële druk is;
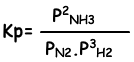
De relatie tussen deze twee evenwichts constanten is;
Kp=Kc(R.T)Δn
Δn= Σnreactanten - Σnproducten
Bijvoorbeeld:
N2(g) + 3H2(g) ↔ 2NH3(g)
Sinds Δnproducten=2 (2 mol NH3) and Δnreactanten=4 (1 mol N2 and 3 mol H2)
Δn= -2
Kp=Kc.(R.T)-2