Gassen Examen 3 En Probleem Oplossingen

Gassen Examen 3 En Probleem Oplossingen

1. Zoek een volume van 0,5 mol CH₄ onder een druk van 3,28 atm en een temperatuur van 400 ⁰K.

Oplossing: P=3,28 atm, n=0,5mol, T=400 ⁰K, R=0,082, V=?

We gebruiken de ideale gaswet;

P.V=n.R.T

3,28.V=0,5.0,082.400

V = 5 liter

2. Als 6,4 g CH₄ een druk heeft van 0,5 atm en een volume van 2 liter, zoek dan een druk van 9 g C₂H₆ met 1 liter volume onder constante temperatuur. (C = 12, H = 1)

Oplossing:

We vinden eerst de mol van gegeven zaken; n_CH4=6,4/16=0,4mol

n_C2H6=9/30=0,3mol

Omdat de temperatuur constant is, schrijven we de ideale gaswet zoals hieronder aangegeven;

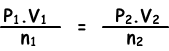
(0,5.2)/0,4=(P₂.1)/0,3

P₂=0,75 atm

or P₂= 57 cm Hg

3. Zoek dichtheid van O₂ onder 27 ⁰C temperatuur en 1,23 atm druk. (O = 16)

Oplossing: T=27 + 273=300 ⁰K

Als we ideale gaswet voor dichtheid schrijven, krijgen we de volgende vergelijking;
d=(P.M)/(R.T)

waarbij M een molmassa van O₂.

d=(1,23.32)/(0,082.300)

d=1,6g/liter

4. Als we de kranen openen die in de onderstaande afbeelding worden weergegeven, zoek dan de eindtemperatuur van gassen.

Oplossing:

We gebruiken de volgende vergelijking om de uiteindelijke druk van het gasmengsel te vinden;

P₁.V₁ + P₂.V₂ + P₃.V₃ = P_final.V_final

3.2 + 4.3 + 0.5 =P_final.(2+3+5)

6 + 12=P_finall.10

P_final=1,8 atm

5. Wanneer we de kranen openen die in de onderstaande afbeelding worden weergegeven, vinden we veranderingen in de druk van gassen.

Oplossing:

We moeten de uiteindelijke druk van het systeem vinden om een vergelijking te maken.

P₁.V₁ + P₂.V₂ + P₃.V₃ = P_final.V_final

P.V + 2P.2V + 3P.V = P_final.(V+2V+V)

P_final=2P

Dus,

I. Druk van verhoging eerste container

II. De druk van de tweede container blijft constant

III. Druk van derde container neemt af