Ideal Gas Law with Examples
Ideal Gas Law
In ideal gas; molecules have no volume and there are no interaction between them. In real there is no such a gas, it is just an assumption. All real gases has small volumes and there are interactions between them. In problem solutions; we assume all gases as ideal gas. Given equation below is ideal gas law. We get it by combining all gas laws given in last section.
P.V=n.R.T
Where; P pressure, V volume, n number of particles, R gas constant 0,08206 L atm / K mol or 22,4/273 L atm / K mol, and T temperature
Now we solve some problems related to ideal gas law for better understanding, follow each example carefully.
Example: Find pressure of 8,8 g CO2 at 27 0C in container having volume 1230 cm3. (C=12, O=16)
Solution: We first find molar mass of CO2;
CO2=12+2.16=44
Then, we find moles of CO2;
n=8,8/44=0,2 moles
Converting temperature from 0C to K and volume from cm3 to liter;
T=27+273=300 K
V=1230 cm3=1,23 liters
Now, we use ideal gas law to find unknown quantity.
P.V=n.R.T
P.1,23=0,2.0,08206.300
P=4 atm
Example: Find molar mass of X(gas) given in the picture below having volume 896 cm3, temperature 273 0C and mass 0,96g. (O=16, and atmospheric pressure is 1 atm )

Solution:
We make unit conversions first.
P=38 cm Hg=38/76=0,5 atm
V=896/1000=0,896 liters
T=273 + 273=546 K
Now, we use ideal gas law to find n;
P.V=n.R.T
0,5.0,896=n.(22,4/273).546
n=0,03 moles
Molar mass of X;
MX=mX/n=0,96/0,03
MX=32 g/mol
Thus; X(gas)=O2
Example: System given below is placed in a location having 70 cm Hg atmospheric pressure. Container has 2 g He at first, then we add 1 g H2 gas to this container. Find the rising of Hg in the manometer after adding H2. (He=4, H2=2)

Pinitial=P0-20=70-20=50 cm Hg
ninitial=2/4=0,5mol He
nH2=1/2=0,5mol H2
nfinal=nHe+nH2
nfinal=0,5+0,5=1mol
We write ideal gas law for initial and final values, then we dive them each other to find unknown value.
V and T are constant in two situations.
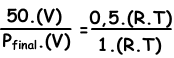
Pfinal=100 cm Hg
Difference between levels of Hg between two branches of manometer;
100-70=30 cm in right branch of manometer
Thus difference between initial and final levels of Hg becomes;
20+30=50 cm
This change is shared by two branches of manometer ;
50/2=25 cm
Thus, Hg rises 25 cm in one branch of manometer.