Ideal Gas Law with Examples

Ideal Gas Law

In ideal gas; molecules have no volume and there are no interaction between them. In real there is no such a gas, it is just an assumption. All real gases has small volumes and there are interactions between them. In problem solutions; we assume all gases as ideal gas. Given equation below is ideal gas law. We get it by combining all gas laws given in last section.

P.V=n.R.T

Where; P pressure, V volume, n number of particles, R gas constant 0,08206 L atm / K mol or 22,4/273 L atm / K mol, and T temperature

Now we solve some problems related to ideal gas law for better understanding, follow each example carefully.

Example: Find pressure of 8,8 g CO₂ at 27 ⁰C in container having volume 1230 cm³. (C=12, O=16)

Solution: We first find molar mass of CO₂;

CO₂=12+2.16=44

Then, we find moles of CO₂;

n=8,8/44=0,2 moles

Converting temperature from ⁰C to K and volume from cm³ to liter;

T=27+273=300 K

V=1230 cm³=1,23 liters

Now, we use ideal gas law to find unknown quantity.

P.V=n.R.T

P.1,23=0,2.0,08206.300

P=4 atm

Example: Find molar mass of X(gas) given in the picture below having volume 896 cm³, temperature 273 ⁰C and mass 0,96g. (O=16, and atmospheric pressure is 1 atm )

Solution:

We make unit conversions first.

P=38 cm Hg=38/76=0,5 atm

V=896/1000=0,896 liters

T=273 + 273=546 K

Now, we use ideal gas law to find n;

P.V=n.R.T

0,5.0,896=n.(22,4/273).546

n=0,03 moles

Molar mass of X;

M_X=m_X/n=0,96/0,03

M_X=32 g/mol

Thus; X(gas)=O₂

Example: System given below is placed in a location having 70 cm Hg atmospheric pressure. Container has 2 g He at first, then we add 1 g H₂ gas to this container. Find the rising of Hg in the manometer after adding H₂. (He=4, H₂=2)

P_initial=P₀-20=70-20=50 cm Hg

n_initial=2/4=0,5mol He

n_H2=1/2=0,5mol H₂

n_final=n_He+n_H2

n_final=0,5+0,5=1mol

We write ideal gas law for initial and final values, then we dive them each other to find unknown value.

V and T are constant in two situations.

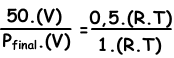
P_final=100 cm Hg

Difference between levels of Hg between two branches of manometer;

100-70=30 cm in right branch of manometer

Thus difference between initial and final levels of Hg becomes;

20+30=50 cm

This change is shared by two branches of manometer ;

50/2=25 cm

Thus, Hg rises 25 cm in one branch of manometer.

Gases Exams and  Problem Solutions